Free Time Research

3.4 Amacrine Cells Do the Rest of Work

Amacrine cells, like horizontal cells, are a type of interneurons in the retina. They forms a large family of many subtypes with various shapes and sizes. Their most prominent feature is the great arborization of dendritic trees to cover small to large visual fields, depending on their tissue locations. Amacrine cells are strictly either mono-stratified or bi-stratified in the IPL region, where the axon terminals of bipolar cells and the dendrites of ganglion cells interconnect. Meanwhile, they make extensive and intricate connectivity to other cells in their reaches. Amacrine cells perform important functions both in local and global scopes.

​

After visual signals enter bipolar cell layer, N bipolar cells with hyperpolarization signals are ready for conversion into the neural wavelength λ, while P bipolar cells with depolarization signals are ready for conversion into the neural intensity ί. Both conversions will take place independently in the sub-lamina space in their own channel with the help of amacrine cells sitting in between.

​

Neural λ is produced by dividing lambda 𝝂s (Equation (2)), and neural ί is produced by subtracting lambda 𝝂λs (Equation (4)). Here division and subtraction are operations borrowed from mathematics to make a point that 𝝂s of a lambda pair will be combined in certain ways to generate new membrane potentials in the ganglion cells. Output of λ and ί must be predictable and precise in quantity, time, and space for every input of 𝝂 and 𝝂λ. This two processes, similar to lambda pair matching and lambda effect resolution, must be instructed by their own algorithms – λ algorithm for λ generation, and ί algorithm for ί generation.

​

In fovea execution of λ algorithm occurs in sub-lamina a, where the axons of N bipolar cells contact dendrites of N ganglion cells. Execution of ί algorithm occurs in sub-lamina b, where the axons of P bipolar cells contact dendrites of P ganglion cells. λ algorithm is independent of ί algorithm, but ί algorithm might require input of signals produced by the λ algorithm. Since hyperpolarization signals reach the sub-lamina a earlier, the execution of λ algorithm could occur ahead of ί algorithm.

​

Contacts between bipolar cell axons and ganglion cell dendrites form a large number of synapses, as both axons and dendrites are quite arborized. When the neural signals reached the branching points on bipolar cell axons, they could be partitioned into each axon terminal. Each axon terminal could carry its own threshold to control if the signal it received sufficed to release neurotransmitters into the postsynaptic cells. Amacrine cells, integral part of the algorithms, would influence greatly the outcome of the algorithms. The central role of amacrine cells could be to either strengthen or weaken the signal that flows from bipolar cells to ganglion cells. The nature of the outcome could be further influenced by information amacrine cells received from other amacrine cells and/or bipolar cells or ganglion cells. Only survived signals could release neurotransmitters to act on postsynaptic dendrites of the ganglion cells. With their large number of subtypes to cover various visual fields in different locations, amacrine cells could exert broader influences in the visual pathway beyond λ algorithm and ί algorithm, for example, coordinating, integrating, and synchronizing visual signals from large visual areas to enhance the overall quality of color vision. The ganglion cells finally summate the signals from their dendritic trees into final bits of information in axons and transmit them to the central brain.

​

Although the neural division and neural subtraction could be complicated, both would follow the steps set by λ algorithm and ί algorithm respectively. As a result, the end products are predictable from time to time, and the time consumed to execute the algorithms are constant from time to time as well. Only through the operations of high precision nature, visual signals from different processing sources can be synchronized and integrated to the highest degree possible across the entire retina, which makes the entire visual field as a uniform whole.

​

To this end, the visual signals that originate from a lambda pair of cones in the fovea finally enter the four ganglion cell axons, two carrying the identical λ and two carrying the identical ί. There should be only one λ and one ί for the entire H cluster. They are the ultimate signals of color vision for the visual cortex to perceive the world in full color. Should the visual signals λ and ί carry the same sign as all positive or negative, they could confuse the visual cortex to mistake λ for ί or vice versa where they are combined and translated into colors.

​

4. One Dimensional Senses and Two Dimensional Senses

There are generally five senses in higher animals to collect information from the environment, vision, hearing, taste, smell, and touch. They can be further divided into two groups, one dimensional sense group or group one, which includes taste, smell, and touch, and two dimensional sense group or group two, which includes vision and hearing. The fundamental difference between these two groups is whether a single factor or two factors determine the nature of the neural signals that the central brain depends on to accurately perceive the external stimuli.

​

The external stimuli of the group one are usually chemicals that act on sensory cells that line the surface of a sensory organ to generate nerve impulses as responses. In the central brain the nerve impulses from the entire sensory organ are processed as a whole unit, not based on individual signals, to produce a single sense of the stimuli. The senses produced from kitchen vinegar are a good example to illustrate this. Vinegar is an aqueous solution of acetic acid. It displays a pungent smell to the olfactory cells and sour taste to the taste buds. Among human olfactory receptor family, one or more olfactory receptors can bind acetic acid molecules with different affinities and elicit neural responses of different degrees. The sense of smell will be stronger for receptors with higher affinity for acetic acid and weaker for receptors with lower affinities. The same happens to the taste buds. Nevertheless, the central brain will not distinguish which signals originate from receptors with higher affinity for acetic acid, and which signals are from the receptors with lower affinity for the acid. The smell of vinegar is the perception of aggregated presence of all the nerve signals arrived at the olfactory processing center from the nose without need to know the exact nature of individual nerve signals and the olfactory receptors that produced them, even though the degree of smell is proportional to the total number of olfactory receptors stimulated by the acetic acid molecules regardless of their binding affinities.

​

In general, perception of smell or taste or touch is the collective result of all the signals received from the entire peripheral sensory organ as a mixed whole without the need to decode each individual signals from the sensory cells. What matters is the concentration of chemical stimuli, the total number of stimulated cells, and the average affinities of all receptors for the chemical stimuli expressed on the sensory cells. More intense the average signals produced in the sensory organ, stronger the sense or perception generated in the brain, and higher sensitivities to the stimuli. Therefor, the sense of the group one stimuli is one dimensional, depending only on the collective amount of signals received, not on individual signals in the signal pool. In other words, the resolution of perception of smell, taste, and touch is on the level of the sensory organ, not individual signals and their producing cells.

​

One dimensional senses have evolved over a billion of years for the animals to perceive the presence of some chemicals or physical objects in the environment and respond accordingly. The sense of smell is especially critical to animals, especially to those that are solitary or have compromised vision, during mating seasons, hunting, danger detection, movement, familial member recognition, etc. It’s obvious that in all these applications the overall sensitivity of the olfactory system matters most as animals rely on such a system to detect even a trace amount of chemicals like pheromones produced and released into the environment by other animals. Clearly this isn’t dependent on the details of individual signals among all responses from the olfactory system, but total amount of signals that reach the central brain from the nose.

​

Vision and hearing are group two senses that perceive physical entities, light and sound. A fundamental characteristic of the perception of physical entities is to form an image or sound in the central brain that exactly mirrors the external scene or sound, not just to generate a simple sense like smell being awful or taste being sweet. Perception of light or sound is actually the perception of color or sound wave, while color and sound wave are determined by the dual properties of wavelength and intensity. The intensity of group two is equivalent to the concentration of chemical stimuli in group one, however, every bit of the signal matters as it is the neurological representation of a particular point in the external visual scene or sound. Therefore, misrepresentation or deletion of one or more signals will corrupt or disrupt the entire scene or sound, thus forming an incomplete or distorted image or sound in the brain. Furthermore, all the signals arrived at the central brain must agree with the original scene or sound in spatial and temporal arrangement. In other words, any signals can’t mix with other signals and must keep their own neurological identities in the peripheral and central brain. As a result, the amount of information for vision and hearing is far more overwhelming than for simple smell and taste. This raises a few basic questions. Are all-or-none universal action potentials sufficient to carry all the information for vision or hearing? Does each sensory cell have only one single signal transduction pathway to convey signals it produces to the central brain? Does the central brain require separate information about wavelength and intensity when perceiving color or sound? If yes, how and where are the light or sound signals decomposed into wavelength signals and intensity signals, in the sensory organ or central brain?

​

​In mammalian auditory system, two types of hair cells in the inner ear are responsible for hearing. Most information about sound reached the brain via the inner hair cells, while the role of the outer hair cells is less clear despite over three times more numerous than the inner hair cells. Inner hair cells act as the mechanoreceptors for hearing: they convert sound frequency into electric activities and transmit them to the central nervous system. The function of the outer hair cells is now perceived as a sound amplifier by refining the sensitivity and frequency selectivity of the mechanical vibrations of the inner hair cells, thus likely determining the loudness in a frequency specific manner. Could the evolution of inner and outer hair cells be considered a coincidence like the presence of the dual channels in the visual system? The likeliness as a coincidence is small, but the electric signals for wavelength and intensity are indeed separated from each other for vision and hearing.

​

On the two dimensional coordinate system, let x axis be set for wavelength and y axis for intensity. Any point on the system defines the color or sound that corresponds exactly to one stimulus of the original signal source that falls on retina or inner ear, while all the points on the system constitute the entire scene or sound in a given moment of time. The positions of any points on the system are fixed relative to their neighboring points, and their neurological interpretation by the central brain can be different from their neighboring points as well. In other words, all the signals on the system constitutes an image of a visual scene or all sounds that enter eye or ear in a given moment of time. Such as coordinate systems must be present in the central brain in the visual cortex and auditory cortex as a mirror copy of the peripheral systems. A time series of such a coordinate system make up what we see or hear during the time covered by the time series, for example, a video or song clip. Therefore, vision and hearing are said to be two dimensional senses. In contrast, nerve signals for smell, taste, and pain can’t be plotted onto a two dimensional coordinate system, but a one dimensional coordinate system.

​

​Another fundamental difference between the two groups of senses is on the memory level. Human taste buds can distinguish many different tastes. If a drink contains honey, you will immediately recognize it contains honey after a small sip of it. Humans can recognize a variety of food or chemicals based on their tastes in blind taste tests. However, can you project the honey taste in your brain when you are thinking of honey? Similarly can you project the smell of vinegar or a certain fragrance, or the pain of a prickle on the skin in your brain when you are thinking of them? The answer is a clear no. Human brains are unable to generate the senses of smells, tastes and touch in the central brain in the absence of chemical or physical stimulation of the sensory organs. A possible explanation is that group one senses are hard to define precisely in terms of nerve signals as they are treated as a whole, not individual signals, posing difficulty of how and what portion of the signals to store. What the central brain can do best seems to store a minimum amount of information that is just enough to reminder the brain that the incoming signals are from olfactory receptors or taste buds or pain sensors, and what smell, taste, or pain they are.

​

​On the other hand, an image or sound can appear in human brain in the absence of stimulation of the real object or sound that appears in the brain. For example, you can project an image of rose or play a song in your brain. In this case, the image or sound must be stored in the memory in early experiences.

​

​Human thinking is actually the result of the silent sound in the form of human language endlessly going throughout a thinking process. More importantly, the sound is the replay of a tone in the brain that the individual knows. For example, the tone of someone’s voice, a particular car’s engine, a bird song, etc. The sound in the replay is silent and flat, meaning the loudness of the sound can’t be raised or lowered. The tone of a sound is determined by the sound wavelength, suggesting that the wavelength from a given sound source is stored in the memory, while the loudness or amplitude of any sound source isn’t. It makes sense that it is unnecessary to record the loudness of a sound as the loudness is a general characteristic of sound applicable to all the sounds. An implication of the sound replay is that the sound signals originated in the ear are separate in two types in the central brain, one encoding wavelength for the tone and one encoding amplitude for loudness. Only wavelength part of the signals forms memory, while the amplitude is lost after its use. An immediate question is that where the nerve signals for the sound are separated into two types, in the ears or in the central brain? A logic answer is in the ear as the ear has the first hand information about the physical dual properties of the sound. The presence of inner hair cells and outer hair cells seems to be a must for bringing sound into the central brain not only for perception, but also for memory storage. If evolution didn’t make inner and outer hair cells, it would make other cellular structures to fulfill the same functionalities.

​

The similar situation is less clear for vision. Like hearing, the presence of the dual channels and super ribbon triad structures in one channel isn’t a pure coincidence as well, but a must for bringing light into the central brain for perception. However, is it necessary for memory storage? It seems uncertain which visual signals, wavelength or intensity or both is stored in memory for future image projection. Unlike sound replay in which tones are clear, accurate, and flowing unbroken for easy recognition, and even enjoyment, the image projected from memory is unclear and distant with poorly defined boundary and shapes. It requires effort of mental concentration to project as the image will disappear quickly after concentration is eased. Can you project color red in your brain? Does the flower rose projected from the memory have the color of dark red like a natural rose the eye sees? The projected image is dull regardless even if it is in color. Unlike sound amplitude which is a general factor to alter the level of the tone, the intensity of light is one of the two deterministic factors for the color as shown in Figure 3. An immediate question is that which visual signals from the memory, λ or ί or both, are used to project images in the brain? Or which visual signals, λ or ί or both is stored in memory?

​

How an image is created? By observing maple tree leaves from spring to fall, we found that all leaves remain in the same shapes, but their colors are changing as seasons change. The surface of a leaf reflects the light into our eyes, resulting in a leaf shaped area on the retina being stimulated and then generating an image of that leaf in our brain. While the same leaf reflects light into our eyes, always forming the same shaped leaf image, color changes in different reasons cause leaves to reflect light of different wavelength into our eyes, resulting in the same leaf image with different colors. It can be concluded that it’s the quantity of photons or intensity, not wavelength of the photons, that delineates the shape of an image. In other words, it’s the area in the retina that is hit with photons defines the bounds of an image, while wavelength is only an attribute of light that gives the image colors. The same wavelength will confer any shaped surfaces the same color as the same paint will paint any surface to the same color.

​

​Regardless, memory based image projection and the anatomical structure of retina substantiate the conclusion that the visual signals have diverged into separate signals for wavelength and intensity along the signal transduction pathway prior to their entry into the central brain. And the two types of signals are treated differently in terms of memory storage. The wavelength determines the base color, while intensity determines the brightness of that base color in quite dramatic way. The combination of wavelength and intensity generates millions of colors human eyes can distinguish. Nevertheless, it’s the intensity that finally determines the shapes of a physical objects in addition to color, and it’s logical to think that wavelength and intensity shouldn’t be stored as single signals, but separate signals for the color. It is certain that ί is the visual signals for physical objects that are stored into memory and it’s also the memory source to project images of the physical objects. The two dimensional senses are more than generating an overwhelming amount of information for best perception, they also expose another layer of mystery how the central brain processes and store information gathered from the surroundings through vision and hearing.

​

Nerve signals from the one dimensional peripheral sensory organs are stored in memory as concept memory, while for nerve signals derived from the two dimensional peripheral sensory organs, one dimension is stored as concept memory and the other as physical memory. Only physical memory can be retrieved to project the original senses. Earlier discussion indicates that the nerve signals that represent light intensity and sound wavelength are stored as physical memory, while the nerve signals representing light wavelength are stored as concept memory. Nerve signals for sound amplitude may not be stored at all.

​

Existence of concept and physical memories reveals different memory mechanisms at work in the central brain. If we dig a little deeper, we can ask a very basic question how many memory neurons are engaged in memorizing the pungent smell or sour taste of vinegar, or the color red? If you looked at a small red circle and a large red square, your brain formed memory for the shapes of circle as well as square, but how could your brain form memory for the color red? Color is like smell or taste or pain except that color can’t exist on its only, but always attached to a physical object. The red on the circle and square are the same, so the nerve signals that represent them. Should the nerve signals of different origins for the color red be stored in separate memory spaces in the memory? If this was the case, then color red would be stored in memory millions of time after we looked at red color millions of time. For concept memory, therefore, a small number of neurons suffice to mark the smell of vinegar or color red, and the nerve signals from identical stimuli like color red or vinegar will be stored only once. An advantage of the concept memory is store once and use everywhere with the same smell, taste, pain or color, a clear approach to save memory neurons and avoid redundant storage. A critical issue is that the memory must store concept information enough to distinguish one concept from vast other concepts stored in memory. In contrast, physical memory stores a concrete physical entity which has bounds and details, thus requiring more neurons to store.

​

​The purpose of this section is to provide additional neurophysiological evidence to substantiate the conclusion that the raw visual signals separate into λ and ί, not only for the best accuracy and acuity, but also for memory storage.

​​

5. Conclusions and Discussion

This paper is intended to explain how the color vision works with an emphasis on the central vision. Visible light possesses two independent physical properties, wavelength and intensity. In color theory, hue, along with saturation and brightness, makes up the three distinct attributes of color. Hue is related to wavelength of visible light, and the brightness depends upon the amount of light falling on a surface, which is proportional to the amount of light emitted from a given color source. Saturation pertains the amount of white light mixed into a hue. A fully saturated color is any spectral color that consists of only one wavelength. Saturation reflects the degree of how mixed the wavelengths of light are. In a sense, both hue and saturation are related only to the wavelength of light. The composition of wavelengths is intrinsic to the light emitted from given sources, but the intensity can vary as the power of light sources vary. Because color is perceived by the eye, the dual properties of light must be the two fundamental factors the eye relies on to achieve color vision. Therefore, the cellular and molecular basis for color vision is predicted to generate the neural forms of wavelength and intensity for the central brain that represent the physical wavelength and intensity, respectively.

 

Retina is a fascinating masterpiece created by mother nature. The simple, raw signals that start from light exposure in the photoreceptors undergo a long and baffling journey to finally end up in the central brain. In this journey the retina does all the nuts-and-bolts kind of signal processing jobs with only one goal: to reduce the primitive visual signals – electric membrane potential 𝝂s – into wavelength and intensity needed for color vision. Let’s look at the Equations (1) to (4) again in one place:

​

​

​

 

 

 

​

​

​Equations (1) to (4) lay the architectural blueprint of the cellular structures for color vision, and the primate retina is the biological implementation of Equations (1) to (4). Equation (1) requires two cell types with different sensitivities to the same wavelength to produce a pair of electric membrane potentials – lambda 𝝂s. In primates, M-cone/L-cone pair and S-cone/M-cone pair fulfill Equation (1). Equations (2) and (3)/(4) dictate the generation of λ and ί in separate spaces and neuronal operations, respectively. In primates there exist two channels, N channel for processing and conducting λ signals, and P channel for processing and conducting ί signals. Equation (3) requires that the initial electric membrane potentials 𝝂s be modified in certain way for Equation (4). In primates, 𝝂s are modulated first into 𝝂λs in the super cellular structure ribbon triads before they are used as input for ί production in sub-lamina b. Upon implementation of Equations (1) to (4), the primate retina has achieved the capability of full color perception. It first converts light into raw electric membrane potential 𝝂s in the cones and then reduces 𝝂s back into neural forms of the wavelength λ and intensity ί via two signal transduction pathways composed of bipolar cells, ganglion cells, and accessory horizontal cells and amacrine cells. λ and ί are the final input to the central visual cortex for color vision.

​

When light enters the eye, it strikes individual cones to produce electric membrane potentials, the initial visual signals 𝝂s. 𝝂s are the sole raw signals left by light stimulation. Because of different sensitivities of the visual pigments in the cone cells to the same light, production of 𝝂s in cones is not sufficient for color vision as 𝝂s aren’t the truthful reflection of the light that entered the eye. Therefore, retina must de-correlate 𝝂s into wavelength and intensity by transforming 𝝂s into signals that truthfully represent light free of bias by removing the effect of cone spectral absorption variations.

​

According to Equation (1), a single cone type can be excited by light of different combinations of wavelength and intensity to produce the same amount of 𝝂s, making it insufficient to differentiate a response change in wavelength from a response change in intensity. The visual information must be obtained by comparing the responses elicited by the same light in two or more types of cones. The complexity of the visual pathway is evolved to work around the principle expressed in Equation (1), and any theories in color vision field should at least be able to give plausible accounts of how different types of cones cooperate to achieve spectral decorrelation.

​

Equations (1) to (4) not only lay the cellular organizational blueprint for color vision, but also equally importantly they establish how physical wavelength and intensity of light will be represented in neural forms free of bias. Based on Equation (1), the initial electric potential 𝝂s are linear and constant to a given source of light, and the ratio of the lambda 𝝂s is a constant, dependent only on wavelength (Equation 2). This can’t be a coincidence as its biological significance is apparent. It has the quality to be the neural form of wavelength or λ that represents the physical wavelength of light for the central brain to perceive hue. On the other hand, the difference of lambda 𝝂s is less sensitive to cone’s spectral absorption variations and can be used to derive the neural form of intensity that represents the physical intensity for the central brain to perceive brightness of light. However, the neural form of intensity obtained in this way isn’t the best to represent the true intensity of light, since the effects of the same wavelength on 𝝂s are not the same in different cone types. The effect of wavelength on lambda 𝝂s is called lambda effect. The retina needs to resolve lambda effect on each 𝝂 of the lambda pair before taking their difference. This difference is the neural form of intensity or ί, representing the physical intensity of light as shown in Equation (4). Resolution of lambda effect is the extra step predicted by Equation (3) that the retina must take to produce ί.

​

In retina, a single cone passes its signals to two bipolar cells. One bipolar cell hyperpolarizes on receiving the signals from the cone, thus negative or N bipolar cell. This N bipolar cell passes its signal to an N ganglion cell in the same fashion. A pair of N bipolar cell and N ganglion cell makes up the negative or N channel. Another bipolar cell depolarizes on receiving the signals from the cone, thus positive or P bipolar cell. This P bipolar cell passes its signals to a P ganglion cell in the same fashion. A pair of P bipolar cell and P ganglion cell makes up the positive or P channel. The cellular structural evidence for the two channels in the retina strongly suggests that visual signals are partitioned into two channels, upholding the presence of the neural forms of wavelength and intensity as predicted by the Equations (2) and (4). Such a dual channel system guarantees that their production doesn’t interfere with each other in space and time. At this point there is no clue which channel is for which form of the neural signal, λ or ί.

​

Equation (3) predicts that there must exist a special cellular structure in one of the channels to resolve lambda effect, and the channel with such a structure is for production of the neural form of intensity ί. A super structure, called ribbon triad, is located at the bottoms of cone axon terminals and controls the gate of the P channel, indicating that it is the site where the lambda effect is resolved and the P channel has been evolved for the ί. The ribbon triad consists of a cone axon terminal, a dendritic tip of a P bipolar cell and two dendritic tips from two horizontal cells. The triad structure is also predicted to be the site where cones across the fovea are matched into lambda pairs. The triad structures make sure that the ί values are produced to the possible maximum accuracy for the best color resolution and acuity. Are the presence of the ribbon triad structure and resolution of lambda effect a pure coincidence? No, it isn’t. If it was, what would be the roles for the triads in visual signal processing? At the triads, primitive visual signals lambda 𝝂s are modulated to become lambda 𝝂λs at the right time just before entering the P bipolar cells.

​

Sandwich algorithm is a hypothesized working model to identify lambda pairs. Lambda pairs that share the same set of 𝝂s fuse into an H cluster, forming a group of cone cells, which are heterogeneous in cone types, but homogeneous in light exposed. A visual scene is delineated into a number of H clusters, depending on its complexity.

​

Further processing of lambda 𝝂s and lambda 𝝂λs in their own channel generates λ and ί, the final formats for the central brain. To this end, all ganglion cells descending from the cone cells in an H cluster carry the same λ in the λ or N channel and the same ί in the ί or P channel. Bipolar cells and ganglion cells seemed to provide a signal passage that allowed horizontal cells and amacrine cells to transform signals into the final formats as they are traveling down through it.

​​

Regardless of sick or healthy, happy or sad or mad, young or old, in cold or hot weather, the perception of the same natural scene is never changed if the scene is not changed physically. The retina is truly a biological computer with extraordinary precision, stability, repeatability, and efficiency. Like a modern computer, the biological computer must rely on some neural algorithms to guarantee that all nervous signals are processed, coordinated, integrated, synchronized, and transmitted precisely, repeatably, and efficiently in input, output, space, and time. At least our neural algorithms – resolve algorithm, match algorithm, λ algorithm, and ί algorithm – are working to guarantee the smooth transformation of visual signals. With the aid of computer simulation technology, it would be possible to simulate some of these neural algorithms to reveal the true nature of color vision.

​

A neural algorithm must be supported by special cellular structures, and a special cellular structure may be evolved to bring a particular neural algorithm into being. The cellular structure could provide a hint of how a neural algorithm would work. The four neural algorithms do show certain structure-function correlations with the cellular structures in the retina where these algorithms are executed. The resolve algorithm is intended to resolve the lambda effect on early visual signals to make the ί values closer to the physical intensity of light. It may incorporate additional information from nearby cones to have a broader evaluation of the signals for better resolution. The underlying super ribbon triad structure forms a special micro-environment in which 𝝂s and additional information received from nearby cones via horizontal cells interact and influence each other to change the amount of glutamate released into the synaptic cleft, thus changing the 𝝂s for the P bipolar cells. The triad structure must maintain a set of neurotransmitter receptors, ion transporters, ion channels, etc with strict on/off threshold values to control the release of glutamate according to the algorithm. Match algorithm is a sorting algorithm acting on multiple cone cells to group them into lambda pairs. Match algorithm relies on the triad as its underlying cellular structure to collect 𝝂s from an area covered by its horizontal cells. Both λ and ί algorithms merge lambda 𝝂s and 𝝂λs to generate new 𝝂s – λ and ί. The underlying cellular structures are dense axon-dendrite connections, and the connections are heavily intertwined with amacrine cells, the accessory cells between OPL and IPL. These structures can support extensive communication between individuals of the lambda pair, partition signals along the axon and dendrite tree terminals for micromanagement, and provide the means to exchange information with local and global bipolar and ganglion cells for coordination, integration, synchronization, and so on.

​

Separation of visual signals into λ and ί have great advantages in signal processing. If there was only a single channel, for example, the widely accepted ON channel (see below) to process, carry, and convey visual signals, would the eye be able to distinguish a million of colors, most of which differ only subtly or barely detectably? The answer is a definitive no because the all-or-none action potentials are too narrow in their range to distinct signals which differ in all degrees, tiny or big. However, separation of signals into λ and ί confers visual system a combinatorial power to double the capacity to produce and conduct visual signals in more granulate details. In addition, the dual channel system allows production of ί in its own processing space, thus broadening the ί range without impact on λ, and enhancing the visual sensitivity to tiny changes in intensity. Lastly because λ is chromatic and ί is achromatic, the central brain can perceive colors by adding chromatic λ to achromatic ί much like adjusting achromatic paint to desired color tone by adding more or less chromatic solvent. Color comparison is made more easily and precisely by comparing λ with λ, and ί with ί.

​

Physics of visible light, cellular structures of the fovea area in the retina, the necessity of multiple types of cones for color vision are all hinting a scheme of visual information flow that starts from the cones and ends at optical nerve described by Equations (1) to (4). A theory in color vision must address the possible roles and action of each of the cellular structures and components present in the visual system and provide reasonable account for how different types of cones work to resolve 𝝂 changes caused by wavelength or intensity, and how weakly absorbed red light is perceived as brightly and vividly as strongly absorbed green or yellow light. Otherwise it isn’t a theory per se and has no value in science.

​

In a logical design of workflow, each step is given a specific task to accomplish. The later step will continue what’s left by the earlier steps and won’t repeat the tasks completed by the earlier steps unless there is a need to repeat. All living organisms are highly efficient in utilizing the resources available to them, and the retina won’t be exception. Visual pathway isn’t long, consisting of a cascade of only three cells of different types, which enables the visual signals to be processed in a highly sequential and logical order along the pathway. It’s expected that each cell type has its own special roles in this logic workflow that other cell types don’t have, ensuring that the signal processing is a stepwise process with each step accomplishing a specific task, and that the later cell types in the pathway won’t be possibly performing any tasks already performed by earlier cell types.

​

A logic order of visual signal processing would be likely in an order of local scope to global scope. The earliest step generates the raw 𝝂s upon light exposure. When the cone cells pass 𝝂s to bipolar cells, early transformation happens, but it is limited to the local scope just to do what early step can do in the pathway. It would be illogical to think that the raw 𝝂s would be modified in an all-around fashion in this early time before other relevant information was available from wider areas, as this could bear serious consequences of distorting the color. A logical work in this transformation is to partition the raw 𝝂s into N bipolar cell and P bipolar cell, respectively, making ready for the generation of λ and ί in the next step in the pathway. Partition of the raw 𝝂s must be done in the early time in this workflow, as delay will lead to signal contamination and loss of signal identity. Resolution of lambda effect must be done here as ί production must be in sync with λ production. This early transformation doesn’t require collection and integration of information from cones located far away.

​

After the raw 𝝂s are partitioned into N and P bipolar cells, transformation of 𝝂s into λ and ί follows immediately since production of λ and ί must depend only on the 𝝂s directly from the cone cells to ensure that neural forms of wavelength and intensity are genuinely reflecting those of the light. This is especially essential for λ as λ is the base color which will paint the ί to generate color. Therefore, production of λ and ί is local as well.

​

Signal transformation is local and ends upon the completion of production of λ and ί. Only when λ and ί pass down through the later part of the logic workflow in their own channel, it makes sense for the neural form of intensity to subject to further modulation in a global scope. Global scope means the need to collect processed information from a large number of bipolar cells and ganglion cells from a broad area and use this information to evaluate and then make necessary modulation to the ί values so that the ί fits well in the visual scene. In the case of possible contrast enhancement, which obviously is a global action, the retina must first know what visual signals are involved in contrast and when they are available for comparison in order to adjust and enhance the contrast. Therefore, only when the global scope signals are available in the later steps of the logic workflow, signal modulations like contrast enhancement can occur if they are part of the visual processing pathway.

​

Color perception under the same lighting condition is consistent in any moment of time. Because of this, a coefficient can be proposed to describe the phototransduction pathway and express a quantitative relationship between generation of transmembrane electric potentials, photon absorption rate, and the number of photons hitting a cone in a unit of time as Equation (1). Equation (1) is the base equation from which Equations (2) to (4) are derived. Equations (1) to (4) establish a theoretical logic workflow for visual signal processing, which agrees well with what has been discussed earlier, which is based on observations on molecular and cellular structures of the retina and electrophysiological study conducted during light stimulation. It’s particularly interesting that Equation (3) predicts the existence of an extra cellular structure in the visual pathway required for ί generation. All this can’t be a coincidence, but is what exactly happens in the visual perception of color.

​

The processed visual signals λ and ί converge into the optical nerve where they are dispatched to the visual cortex in the central brain. When nervous impulses enter the central brain from the peripheral, they have entered a totally different world, where they all have lost their identity and individuality like a drop of water mixed into a pond. They form a whole with all the other nervous impulses from the peripheral. In the central brain, the whole is much much greater than the sum of its parts, resulting in the impossibility to trace the origin of each of the individual impulses in the whole to the peripheral. It must be cautious in attempt to establish what happens in the peripheral by extrapolating from what we all are experiencing in the central brain, as the conclusions or results are more likely to misguide and, as a result, hinder research.

​

N bipolar cells are called OFF center bipolar cells and P bipolar cells ON center bipolar cells in the research literature, and same for ganglion cells. ON center bipolar cell and ON center ganglion cells make up the ON center channel, and OFF center bipolar cell and OFF center ganglion cells make up the OFF center channel. Furthermore, Off center cells and ON center cells form a center surround organization in a configuration of color opponent centers and surrounds (red/green) and ON or OFF centers and surrounds. The concept ON/OFF center surrounds and color opponent center surrounds is too overly complicated and abstract to be true in retina. It’s hard to apprehend what possible concrete roles the center surround organizations and ON/OFF center channels could serve in color vision, especially in terms of wavelength and intensity, super ribbon triad structure, L-cone/M-cone pairs for color resolution, and perception of spectrtally weak light. Why does a cone diverge its signals into ON and OFF center bipolar cells? What nature are the signals in the ON and OFF center channels to color vision? In individuals with normal color vision the ratio of L-cone to M-cone can be off 1:1 mark considerably to 10:1 or 1:10, or worse. An inference is that a cone of one type can’t be surrounded by cones of other types in individuals with off-mark ratios. The rigidity of the center surround organization is also at odds with the unlimited capacity to respond to all natural scenes from surroundings. The center surround organization is established largely on data obtained from intracellular and extracellular recordings of bipolar and ganglion cells, hence its validness is highly questionable. However, these theories have become the foundation of color vision research. Research based on wrong theories is detrimental because it can misguide experimentation, thinking, and interpretation, all of which can impede the progress in our understanding of color vision.

​

More importantly in phototransduction, light stimulation turns photoreceptors hyperpolarized. Are light stimulated photoreceptors OFF? Hyperpolarization is simply a neural state after a neuron is exposed to certain external stimuli. As long as an hyperpolarized state could impact downstream neurons, it should not be considered OFF. Furthermore, an OFF neuron could turn the postsynaptic cells ON if receptors expressed on the postsynaptic cells could lead the cells to depolarize upon receiving the pre-synaptic impact. At least in the visual system, the sign of the responses from external or internal stimuli can’t be the determinant factor for responses to be on or off. Calling N bipolar cells OFF and P bipolar cells ON is misleading and improper.

​

To end this paper, let’s use λ values to explain how the colors of multi-wavelength light are determined. Naturally light that enters the eye is not of single wavelength, but of mixed wavelengths. The 11-cis retinal-opsin molecule would absorb any photons in its absorption range. Each wavelength in multi-wavelength light had its own intensity, and stimulated cone cells independent of other wavelengths in the same light. The end result was another 𝝂, the sum of all voltage changes evoked in the cone by each wavelength. That meant the λ would be generated from the lambda 𝝂s derived from mixed-wavelength: 𝝂1/𝝂2 or Ʀ1/Ʀ2, where 𝝂1 and 𝝂2 are composite 𝝂s, and Ʀ1 and Ʀ2 are composite constants. If this λ happened to be equal to the λ generated from the lambda 𝝂s derived from single-wavelength light, the color would be perceived as that single-wavelength color. Because cones discriminate wavelengths only through its retinal-opsin complexes via different absorbance spectra, it would be impossible for the retina to know whether the 𝝂, so the λ, was the result of exposure to single wavelength light or multi-wavelength light. Rather the retina only recognizes the signals it generates, and doesn’t care how these signals are generated and if λ and ί are composite values or not.

​

If light contains two wavelengths that are close in the visible spectrum, like half green and half yellow, the total 𝝂t would be the sum of green 𝝂 and yellow 𝝂. The size of 𝝂t fell between the two 𝝂s if the light contains pure green and pure yellow respectively. The λ value computed from the lambda 𝝂ts fell just within the space close to both green λ and yellow λ, which is an additive color – greenish yellow. On the other hand, if light contains two wavelengths that are not close in the visible spectrum, like half green and half red, the total 𝝂t would still be the sum of green 𝝂 and red 𝝂. The size of 𝝂t again fell similarly between the two 𝝂s if the light contains pure green and pure red respectively. Because the difference between green 𝝂 and red 𝝂 was quite large, 𝝂t would be close to neither green 𝝂 nor red 𝝂, and the λ value computed from the lambda 𝝂ts fell within a space between green λ and red λ, but close neither to green λ nor red λ. As a result, mixing green and red wouldn’t lead to an additive color – greenish red, but a color between green and red, that was yellow. A similar picture could be drawn for light containing blue and yellow. Yellow and green seem to be two chasms in the visible spectrum, and mixing wavelengths from the two sides of each chasm generates colors that fall within that chasm. This is obvious from the visible spectrum. From color opponency point of view, it seems that wavelengths from the two sides of each chasm opposes each other, but actually, it is simply the fact that mixing two dissimilar things lead to a thing that is dissimilar to both of its parents, but stands on its own. There is no such thing as color opponency.

​

Finally an attempt is given to explain how afterimages are produced. The central theme of the dual channel system is that the color we perceive through eye is deduced from the sole products of phototransduction – the electric transmembrane potential 𝝂s – that occurs in M-cones and L-cones. Any visual phenomena must be explained by focusing on what normal visual processes have been disrupted in the retina that caused the visual phenomena in question. If this is not the case, then the cause could be residing in the visual cortex.

​

​Figure 8 illustrates how an afterimage could form after a prolonged exposure to green light. When exposing to green light, M-cone, which absorbs green light more strongly than L-cone, produces a membrane potential 𝝂M, which is greater than the membrane potential 𝝂L produced by L-cone. Upon prolonged exposure to green light, M-cone becomes less sensitive to new color exposure, in this case, the white light. This makes L-cone relatively more sensitive to the white light. As a result, the sizes of the membrane potentials are reversed from 𝝂Mb > 𝝂Lb to 𝝂Ma < 𝝂La, here subscript b means before, and a means after. The direct consequence of this reverse is temporarily shifting λ from green zone into the weak reddish zone, which is perceived as a weak reddish afterimage.

​

​

​

​

​

​

​

 

​

​

​

​

​

​

 

 

 

Changes in the membrane potential 𝝂s in cone cells could result in the changes in neural λ, which changes our perception of color, which underpins the notion that the dual channel system of the retina is at work for the color vision. It must be noted that it can have many plausible explanations for a neural phenomenon because the whole is much greater than the sum of its parts for the nerve system. It doesn’t make sense to fix only on one explanation, while ignoring all other possibilities, even better possibilities.

​

​

​

​

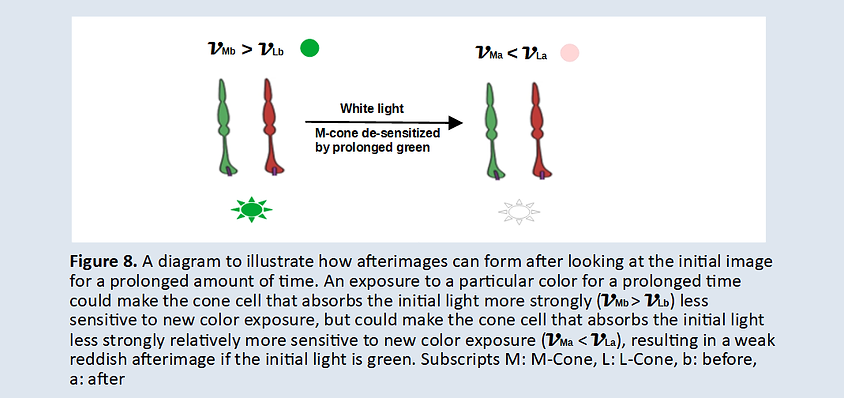
Send correspondence to Hangjiong Chen, PhD, at hjchen1@yahoo.com

 

 

Last updated December 09, 2024

updated January 24, 2023

Updated August 17, 2022

Updated: March 20, 2022

Updated: March 5, 2022

Updated: May 11, 2021

Posted on: March 14, 2021

​